|
7. del
MÅLING

Måling anno 1973 med Brüel & Kjær 1/3 oktav, pink noise.
Kan man bygge højttalere udelukkende baseret på lytning? …eller kan man bygge højttalere udelukkende baseret på computersimuleringer og målinger?
Nej, - det ene udelukker ikke det andet!
Ergo bygning af højttalere er en kombination af beregninger, målinger og lytning. Man kommer således ikke udenom et indkig i måleriets verden, selv her på begynderstadiet, men man må gå lidt på listepoter i starten, når det handler om alle måleteknikkens krinkel-kroge. Erfaringen fortæller, at det for nogen kan virke temmelig overvældende med så megen drilsk teknik og ikke mindst udsigten til investering i en eller anden form for måleudstyr, der jo har ry for ikke at være helt billigt.
Man kan dog starte forsigtigt, uden de helt store investeringer, f.eks. med et enkelt måleområde, der omhandler højttalerens frekvensrespons. Processen kan udføres relativ enkel med en såkaldt Spectrum Analyzer, der er i stand til at yde et rimeligt resultat med en vis margen til det perfekte og samtidig give en forsmag på måleteknikkens virke og funktion. Husk at måling kun er et stykke værktøj, der kan benyttes som et stormasket analysesystem af et lydbillede, hvorimod den menneskelige hørelse har et langt mere finmasket analysesystem og derfor er i stand til at opfatte fine nuancer og detaljer, som stort set er umålelige. Ergo måling vil sandsynligvis aldrig kunne erstatte et ”veltrænet øre” i udviklingsprocessen. Det ”at måle” kan gå hen at blive nærmest en religion og i ekstreme tilfælde udvikle sig til en form for fanatisme, hvor teknikken overskygger alt andet. Her må der prioriteres! - Bygger man højttalere, hvor målingen er det vigtigste eller bygger man højttalere, hvor ørets vurdering er det vigtigste?
Find balancen!
Målesystemerne: Spectrum Analyzere (RTA og FFT)
RTA (Real Time Analyzer) med måleresultater der vises på computerskærmen som søjler. Pink Noise anvendes som et kontinuerligt målesignal, hvilket kan gøre måleresultaterne af selve højttaleren unøjagtige grundet målerummets akustiske bidrag (resonanser, stående bølger og refleksioner). Målerummets akustiske konditioner må derfor, i den udstrækning det er muligt, tilstræbes identiske med det ”lyddøde rum” (anechoic chamber), - dvs. jo større rum, des bedre og desuden rigeligt med absorberende materialer (tæpper, gardiner polstrede møbler o.l.), ligesom lydniveauet på målesignalet fra højttaleren bør være så lavt som muligt, men ikke lavere end det kan differentieres fra uvedkommende lyde.
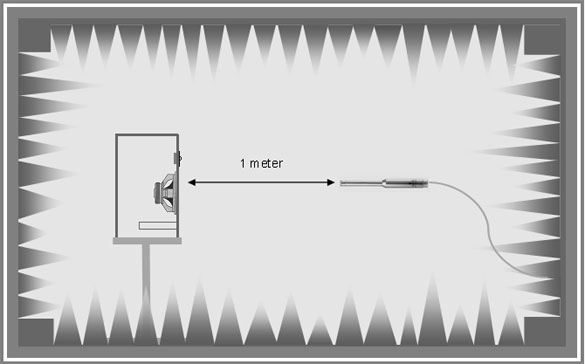
Planche nr. 46 - Lyddødt rum (anechoic chamber).
FFT (Fast Fourier Transformation), navngivet efter Fourier, fransk matematiker og fysiker. FFT fungerer som RTA, men måleresultaterne transformeres og kan i stedet for søjler vises som kurver på computerskærmen svarende til et oscilloscope.
Almindeligvis opfattes et lydsignal i et tidsdomæne, som henholdsvis amplitude og tid, men kan tillige karakteriseres ved dets frekvens. Når et signal skal analyseres kan det derfor være nyttigt at kende den frekvens, der udgør signalet. Denne viden får vi fra at arbejde med signaler i tidsdomænet over til at arbejde med signaler i frekvensdomænet. Og det er netop hvad Fourier transformation gør.
MLS (Maximum Length Sequence), målesignal bestående af korte impulser indeholdende White Noise eller Pink Noise, der sendes til højttaleren via en måleforstærker. I modsætning til det anvendte kontinuerlige målesignal i Spectrum Analyzere er det anvendte målesignal og målingen heraf i MLS systemet af meget kort varighed, hvilket betyder at de reflekterende signaler fra målerummet, grundet lydbølgers lave hastighed, først når målemikrofonen efter målingen af det direkte signal er afsluttet og registreret. Måleresultatet vil derfor ikke i nævneværdig grad påvirkes af den omgivne akustik.
Et enkelt målesystem for begynderen
Følgende anvendes:
-
Program med Real Time Analyzer (RTA), minimum opløsning 1/3 oktav samt generator med Pink Noise, installeres på computeren. Gratisprogrammer til download: RT-Capture www.wavecapture.com eller SynRTA www.libinst.com -
Frekvenslineær måleforstærker på mindst 4-5 watt til at drive måleobjekt.
-
Frekvenslineær målemikrofon, forforstærker samt A/D konverter, tilsluttes computerens USB indgang.
-
Kalibreringer af lydkort og målemikrofon anbefales for opnåelse af højest mulige målepræcision (ej muligt i alle programmer).
-
Skønnet prisniveau: Fra ca. 1.200,- til 1.800,- kroner.
Det må understreges, at systemets målepræcision beror på størrelsen af unøjagtigheder i computerens lydkort, måleforstærker, mikrofon og ikke mindst bidrag fra målerummet akustiske konditioner.
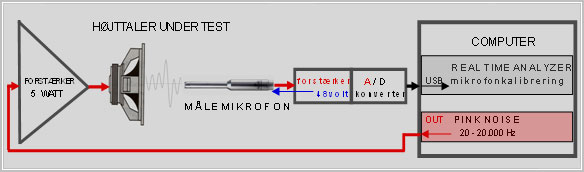
Planche nr. 47 - Måleopstilling: Signalveje: analog = rød / digital = sort. 48 Volt Phantom power = blå.
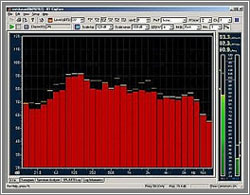 Måleresultater med Real Time Analyzer og Pink Noise vises på skærmen som søjler, der valgfrit kan indstilles til en opløsning fra 1 til 1/48 oktav. Måleresultater med Real Time Analyzer og Pink Noise vises på skærmen som søjler, der valgfrit kan indstilles til en opløsning fra 1 til 1/48 oktav.
NB! RT-Capture gratisprogam muliggør print, men ikke at gemme i computerens hukommelse.
SynRTA gratisprogram kan både printe og gemme.
Hvad er Pink Noise?
Talen om Pink Noise kædes ofte sammen med White Noise, hvilket ikke er så underligt, idet begge signaltyper indeholder samtlige frekvenser i et givet frekvensområde, elektrisk frembragt af en tonegenerator (signalet høres som sus). Forskellen på de to signaltyper skal findes i fordelingen af energimængden.
White Noise har konstant energimængde pr. Hz, - eksempelvis er der lige stor energimængde mellem 20 Hz og 21 Hz som mellem 2000 Hz og 2001 Hz. Frekvenskurven for White Noise er lineær.
Energifordeling:
Oktavinddeler* man frekvensområdet 20 – 20.000 Hz, vil man se følgende opdeling i frekvensbånd indeholdende antal Hz svarende til energienheder pr. oktav, anført i parentes.
1. Oktav : 20 – 40 Hz (20)
2. Oktav: 40 – 80 Hz (40)
3. Oktav: 80 – 160 Hz (80)
4. Oktav: 160 – 320 Hz (160)
5. Oktav: 320 – 640 Hz (320)
6. Oktav: 640 – 1280 Hz (640)
7. Oktav: 1280 – 2560 Hz (1280)
8. Oktav: 2560 – 5120 Hz (2560)
9. Oktav: 5120 – 10240 Hz (5120)
10. Oktav: 10240 – 20480 Hz (10240)
*)En oktav er pr. definition en fordobling af frekvensen.
Idet man i Spectrum Analyzere (RTA) anvender oktavinddelte måleintervaller, vil behovet for en fuldstændig ensartet energifordeling af målesignalet pr. oktav opstå. Med White Noise som udgangspunkt ses en stor ubalance i energifordelingen jf. skema. Ved at sænke energimængden med 3 dB pr. oktav ved stigende frekvens opnås præcis den samme energifordeling i alle oktaver, metoden betegnes Pink Noise. Frekvenskurven for Pink Noise er faldende med stigende frekvens.
Avanceret målesystem for den øvede (kort beskrivelse)
Til de mere krævende, herunder professionelle målinger anvendes hovedsaglig MLS-systemet, der udover program og målemikrofon, forudsætter brug af speciel hardware, der tilsluttes computeren via et ”Fire Wire” interface eller via en hurtig USB port. Skønnet prisniveau: fra ca. 7.000 til 20.000 kroner.
Gratis demoprogrammer, manuals og brochurer m.m.: www.audiomatica.com/clio/download.htm eller www.wavecapture.com
Nedenstående oversigt viser de mest anvendte måleområder:
- Frekvensrespons ret foran (on axis) i nærfelt og afstandsfelt
- Faseforløb
- Forvrængning
- Impedansforløb
- Polar Plot (frekvensrespons i spredningsfelt (off axis))
- Thiele / Small parametre
- Induktion, kapacitet, modstand
Målemetoder:
Nærfeltsmålinger (Near field). Målemikrofon placeres ca. 1 cm fra måleobjekt, f.eks. bashøjttaler, diskanthøjttaler eller portmunding. Fordelene ved nærfeltsmålinger er, at rummet ikke påvirker måleresultatet. Måleresultaterne anvendes til separat vurdering af de enkelte enheders frekvensforløb, resonanser, membranopbrud og roll off ved delefrekvenser som følge af f.eks. filterfunktion samt refleksportens afstemningsfrekvens og output.
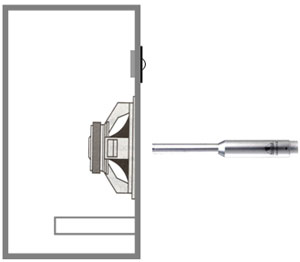
Planche nr. 48.
Fjernfeltsmålinger (Far field). Her begynder det at blive lidt mere kompliceret, idet rummet, som tidligere nævnt, påvirker målingerne i mere elle mindre grad, - især ved lave frekvenser. Udgangspunktet for fjernfeltsmålinger er den såkaldte Time-Window beregning, der ses på nedenstående skitse. Formålet med denne beregning er at kende den ønskede målings startfrekvens, idet frekvenser der måles herunder ikke udelukkende kan henføres til selve højttaleren. Er man ikke i besiddelse af et beregningsprogram for Time-Window, kan det viste eksempel anvendes. Fjernfeltsmålinger anvendes bl.a. til vurdering af en højttalers totale frekvensrespons i frekvensområdet over 200 – 300 Hz.
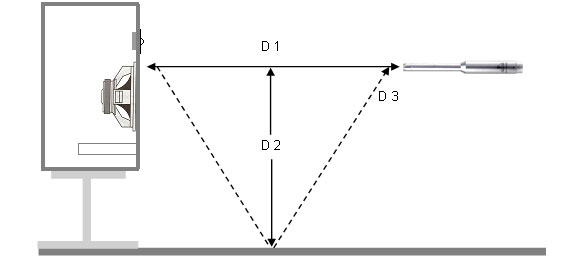
Planche nr. 49.
Eksempel:
D 1: Mikrofonafstand = 1 meter
D 2: Første refleksionsafstand = 1,25 meter
D 3: Total refleksionsafstand (stiplede linier) = 2,693 meter
Time-Window = 4,9346 ms
Måle-start-frekvens = 202,65 Hz
Jo længere refleksionsafstand (D 2), des lavere måle-start-frekvens.
Gulvniveau måling (Ground plane). Måling af en højttaler placeret på gulvniveau kan stort set sammenlignes med måling i et lyddødt rum (anechoic chamber), men idet målemikrofonen opfanger både det direkte og det reflekterede signal fra gulvet er lydtrykket øget med 6 dB. For at kompensere for denne lydtryksforøgelse placeres målemikrofon i en afstand på 2 meter, således at niveauet svarer til det lyddøde rums målinger.
Ved måling af flervejssystemer skal diskanthøjttaleren vende ned mod gulvet og højttaleren tiltes forover (beregning af tiltning se: www.mhsoft.nl/Groundplane.asp).
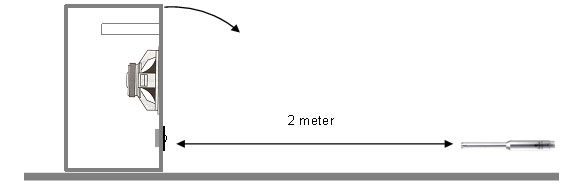
Planche nr. 50.
Spredningsfelt målinger (Polar-plot). Samme måleopstilling af frekvensrespons som i fjernfeltsmålinger, men måling i valgte spredningsvinkler f.eks. 30 og 60 grader.
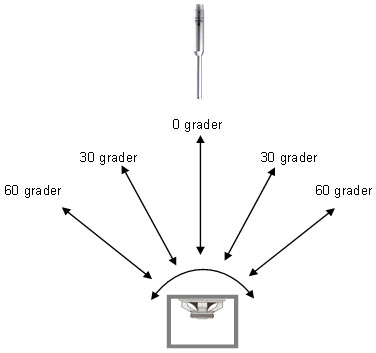
Planche nr. 51.
Måledisciplin
I forbindelse med udviklingsarbejde af højttalere foretages der løbende målinger, hvis resultater kan udlæses på computerskærmen og noteres, gemmes på computeren eller printes. Det er vigtigt at være opmærksom på, at alle måleopstillinger er nøjagtig ens fra gang til gang, idet målemetoderne og heraf følgende resultater, er uhyre følsomme over for ændringer af målesignalets styrke og af måleobjektets placering relateret til rummets akustik samt afstande til gulv- og vægflader. Man må tillige være opmærksom på at genstande, som f.eks. møbler, ikke må ændre position. Dette gælder tillige for mikrofonopstillinger, hvor det bl.a. er særdeles vigtigt at afstand mellem mikrofon og højttaler altid er præcis den samme.
Målemikrofonen
Målemikrofonens egenskaber er vigtige for et godt resultat af måleproceduren. Alligevel kræves der ikke den helt store investering for en ”rigtig” målemikrofon af høj kvalitet.

Måleforstærkeren
Kravene til måleforstærkeren er ikke store hvad angår udgangseffekt, her rækker 4-5 Watt i mono. Til gengæld skal forstærkeren have et fuldstændigt lineært frekvensområde fra 20 – 20.000 Hz, ligesom forvrængning og støj bør være på et absolut minimum. Anvendes der en  standard stereoforstærker med tonekontroller, loudness og filtre, skal forstærkeren indstilles til maksimal lineær gengivelse uden brug af tonekontroller og filtre. standard stereoforstærker med tonekontroller, loudness og filtre, skal forstærkeren indstilles til maksimal lineær gengivelse uden brug af tonekontroller og filtre.
Eksempel - forstærker til indbygning:
- Type: Monacor, IPA 50
- Udgangseffekt: 30 watt, RMS / 8 Ohm
- Forvrængning THD: 0,01%
- Frekvensområde: 20 – 25.000 Hz
- Signal / støj: > 80 dB
- Nettrafo: 230 Volt / 2 x 25 Volt AC
COMPUTEREN
 Computeren har over en årrække udviklet sig til et nyttigt stykke værktøj i forbindelse med højttalerkonstruktion, hvilket vi netop har erfaret her i artikelseriens 7. del, hvor der er gennemgået forskellige måleprincipper. Tidligere i artikelseriens 3. del og 5. del refereredes der til adskillige beregningsprogrammer med simuleringer for kabinet- og filter-konstruktioner. Vi vil i det følgende gå lidt mere i dybden, hvad angår disse programmer, der enten kan downloades gratis eller købes i udgaver med et større udvalg af beregningsmuligheder, simuleringer, grafik m.m. Programmerne stiller ikke specielle krav til computeren. Enkelte programmer findes tillige som gratis demoversioner med en eller anden form for begrænsning. Her får man muligheden til at prøve om programmet opfylder ens behov. Ikke overraskende er købeprogrammerne de bedst fungerende med hensyn til muligheder, hvorimod beregningsnøjagtigheden tilsyneladende er i orden uanset hvilket program man vælger. Computeren har over en årrække udviklet sig til et nyttigt stykke værktøj i forbindelse med højttalerkonstruktion, hvilket vi netop har erfaret her i artikelseriens 7. del, hvor der er gennemgået forskellige måleprincipper. Tidligere i artikelseriens 3. del og 5. del refereredes der til adskillige beregningsprogrammer med simuleringer for kabinet- og filter-konstruktioner. Vi vil i det følgende gå lidt mere i dybden, hvad angår disse programmer, der enten kan downloades gratis eller købes i udgaver med et større udvalg af beregningsmuligheder, simuleringer, grafik m.m. Programmerne stiller ikke specielle krav til computeren. Enkelte programmer findes tillige som gratis demoversioner med en eller anden form for begrænsning. Her får man muligheden til at prøve om programmet opfylder ens behov. Ikke overraskende er købeprogrammerne de bedst fungerende med hensyn til muligheder, hvorimod beregningsnøjagtigheden tilsyneladende er i orden uanset hvilket program man vælger.
Programmerne:
Computerberegninger af kabinetkonstruktioner:
Kabinetprincipper beskrevet i artikelseriens 3. del.
- Trykkammer (lukket system)
- Basrefleks (herunder slavesystem)
- Båndpas (Coupled Cavity)
Her ud over har enkelte programmer også beregninger, om end i et beskedent omfang, af horn- og transmissionsliniekonstruktioner. Beregningerne gælder for bashøjttalere med tilgængelige Thiele / Small parametre dvs.: Resonansfrekvens (fs), godhed (Qt) og ækvivalentvolumen (Vas). Alle tre parametre indsættes i programmet, hvorefter computeren beregner kabinetrumfanget i liter samt portdimensioner, evt. suppleret med grafisk fremstilling af simulerede frekvensforløb, diffraktionstab m.m. NB: Mellemtone- og diskanthøjttalere kræver ikke kabinetberegninger.
De mest simple programmer kan udelukkende beregne det programkonstruktøren kalder ”det optimale” gældende for de tre almindelige kabinettyper baseret på enhedernes Thiele / Small parametre. Beregningerne kan bruges som et udgangspunkt i konstruktionsarbejdet og kan være en udmærket start for begynderen.
Efterhånden som konstruktionsarbejdet skrider frem opstår der hurtigt et yderligere behov for beregningsmuligheder samt grafik med simulerede frekvenskurver m.m. og her kommer man nok til at ty til de mere omfattende programmer, der både findes som gratisprogrammer og købeprogrammer, f.eks. www.lsp-lab.com (findes i en demoversion med 30 dages gratis prøvetid). Se i øvrigt henvisninger til et udvalg af webadresser bagest i artikelseriens 3. del, og endnu flere kan sikkert findes med lidt søgen på internettet.
Sammenligning af beregningsprogrammer til kabinetkonstruktioner:
| Programkapacitet: |
Standard |
Udvidet |
|
Trykkammer
|
|
|
| Beregning af rumfang i liter |
X |
X |
| Bruger-beregning af rumfang |
|
X |
| Simulerede frekvenskurver |
|
X |
| Beregning af dæmpevat i % |
|
X |
| Grafik, simuleret diffraktionstab |
|
X |
| Grafik, simuleret SPL |
|
X |
|
Basrefleks
|
|
|
| Beregning af rumfang i liter |
X |
X |
| Bruger-beregning af rumfang |
|
X |
| Beregning af port, Ø, L, Fsb |
X |
X |
| Bruger-beregning af port, Ø, L, Fsb |
|
X |
| Simulerede frekvenskurver |
|
X |
| Beregning af dæmpevat i % |
|
X |
| Grafik, simuleret diffraktionstab |
|
X |
| Grafik, simuleret SPL |
|
X |
|
Båndpas
|
|
|
| Beregning af forreste kammer i liter |
|
X |
| Bruger-beregning af forreste kammer |
|
X |
| Beregning af bageste kammer i liter |
|
X |
| Bruger-beregning af bageste kammer |
|
X |
| Beregning af port, Ø, L, Fsb |
|
X |
| Bruger-beregning af port, Ø, L, Fsb |
|
X |
| Grafik, simulerede frekvenskurver |
|
X |
| Beregning af dæmpevat i % |
|
X |
| Grafik, simuleret SPL |
|
X |
- SPL = Følsomhed i dB
- Port: Ø = diameter, L = længde, Fsb = afstemningsfrekvens
- Diffraktionstab = Baffelstep
- Bruger-beregninger giver valgmuligheder af individuelle parametre. Programmet beregner herefter de øvrige parametre, - evt. suppleret med simuleret grafik.
Computerberegninger af delefiltre:
Delefiltrenes teoretiske funktioner er beskrevet i artikelseriens 5. del. Husk! - For opnåelse af optimale beregninger af delefiltre bør målinger af enhedernes impedans foretages med pågældende enheder monteret i det planlagte og færdige kabinet. Den udmålte impedansværdi indsættes i filterberegningen. Er man ikke i besiddelse af det nødvendige måleudstyr, kan filterberegningerne dog foretages uden impedansmålinger i kabinettet, i stedet kan man anvende fabriksoplysningerne for de pågældende enheder. Beregningsresultatet må herefter forventes at blive med en større unøjagtighed. Programmernes beregninger, evt. suppleret med grafik med simulerede lydtryk, impedans og fase, er udelukkende tænkt som et udgangspunkt i konstruktionsarbejdet, - ergo må der påregnes yderligere justeringer af filtre evt. suppleret med lytning, nye beregninger og målinger.
Filterberegningen starter med at indsætte de forud valgte parametre i programmet:
- Baffel-dimensioner (højde x bredde)
- Afstande mellem enhedernes centre
- Delefrekvenser
- Højttalerenhedernes impedanser
- Måles efter montering i kabinet
- System: 2-vejs og 3-vejs
- 2½-vejs, 3½-vejs, 4-vejs, 2-vejs D'Appolito og subwoofer.
Herefter foretages valg af øvrige parametre*:
- Filter-orden: 1. orden og 2. orden
- 3. orden, 4. orden samt hybrid
- Filtertyper: Butterworth, Bessel og Linkwitz-Riley
Resultatvisning:
- Diagramtegning
- Grafik med simuleret lydtryk, delefrekvens, fase og impedans.
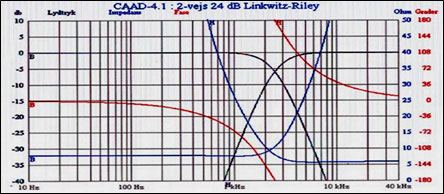
Eksempel på grafik: Sort = Lydtryk / delefrekvens for bas og diskant, Rød = Fase og Blå = Impedans.
Sortiment af ovennævnte punkter varierer fra program til program. Nogle programmer (blå skrift) omfatter således kun de absolut nødvendige beregningsområder, hvis anvendelse gør de beregnede resultater væsentlig mindre præcise. De mere omfattende programmer kan som regel tilbyd hele sortimentet.
*) Øvrige parametre:
Filtrets ”orden”
- 1.orden (6 dB pr. oktav): Simpelt amplitude og faselineært filter uden impulsforvrængning. Det perfekte filter med en enkelt undtagelse, idet filtrets beskedne flankestejlheder giver en ringe dæmpning uden for gennemgangsområdet, hvilket for de fleste enheder er utilstrækkeligt.
Med en rimelig sikker margen på ca. to oktaver ud over gennemgangsområdet kan enheder så vidt anvendes, men her må det konstateres, at det er umådeligt svært at finde enheder, der opfylder så strenge krav til frekvensomfang.
Her ud over vil den effektmæssige beskyttelse af diskantenheder være temmelig ringe, ligesom diskantenhedernes resonanspunkt i mange tilfælde ikke vil være tilstrækkeligt dæmpet, - her kan et LCR-filter (se afsnittet ”korrektionskredsløb”) dog anvendes.
Nødvendigheden af anvendelse af højere ordensfiltre trænger sig på, men inden vi kommer så langt, skal vi lige kigge på et lidt anderledes filter med ”visse” fordele, nemlig et:
- Hybrid (6 / 18 dB pr. oktav) filter, der udelukkende fungerer i tovejs konstellationer og er sammensat af et 6 dB / oktav lavpasfilter med en blød afskæring af bas- mellemtonesektionen samt et18 dB / oktav højpasfilter med en kraftig afskæring af diskantsektionen. Filtret er stort set uden impulsforvrængning og har næsten korrekt højpasfiltrering med effektiv beskyttelse af diskantenheden, men stiller store krav til bas- mellemtoneenheden med hensyn til membranopbrud og afrulningslinearitet, ligesom den amplitudemæssige summering ved delefrekvensen kan være kritisk.
- 2. orden (12 dB pr. oktav).
- 3. orden (18 dB pr. oktav).
- 4. orden (24 dB pr. oktav).
Med disse højere ordens filtre får man løst den omtalte unode i 1. ordens filtret, men til gengæld opstår der så andre unoder med pukler i frekvenskarakteristikken og dermed også i fasekarakteristikken omkring knækfrekvensen (delefrekvensen). Dette kan ikke undgås, men problemerne kan minimeres. Dog ikke alle på samme tid, der må prioriteres og vælges løsninger, som egner sig bedst til formålet. Kompromiser bliver altså nødvendige, ligesom man må være opmærksom på principielle voksende problemer med stigende filterorden, ergo des stejlere flanker, des flere unoder, bl.a. i form af ripple (ringning).
I det følgende ser vi lidt på nogle af de oftest forekommende filtertyper, dog uden at gå i dybden. For de mere videbegærlige henvises til speciallitteratur.
Fagsproget:
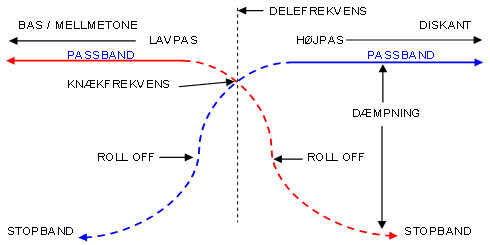
Filtrets ”crossover region” med dets betegnelser.
Filtertyperne:
Alle højere ordens filtre med maksimal flad amplitude kaldes Butterworth, hvor dæmpningen ved knækfrekvensen er 3 dB.
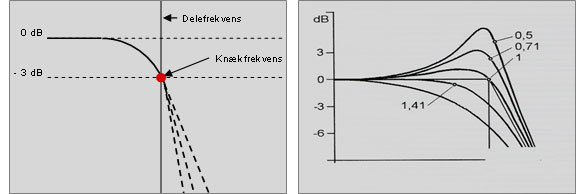
Til venstre: Planche nr. 52 - knækfrekvens. Planche nr. 53 - Til højre: Q-værdiers betydning for ”overhævning”.
Filtrenes karakteristik omkring knækfrekvensen bestemmes af dets ”godhed” betegnet Q-værdien. Eksempelvis har et 2. ordens Butterworth en Q-værdi på 0,71, hvilket bl.a. har at gøre med filtrets flankestejlhed, fasekarakteristik og dermed også filtrets egenskaber relateret til højttalerenhedernes egenskaber.
Til Butterworth filtrets plussider hører maksimal flad amplitude og store flanke-stejleheder. Og til dets minussider hører ripple (ringning), stigende med filtrets orden ved gennemløb af signaler bestående af kortvarige impulser, - eksempelvis musik.
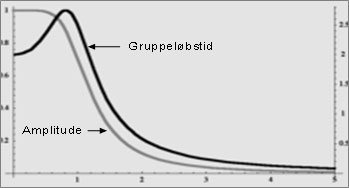
Planche nr. 54 - Butterworth 3. ordens filter: Amplitude (gain) og gruppeløbstid (group delay).
Bessel filtre stiller nok lidt større krav til de anvendte højttalerenheders egenskaber, idet filtrets flankestejlheder (roll-off) er mindre umiddelbar efter knækfrekvensen end f.eks. Butterworth, men slutter alligevel med næsten den samme dæmpning. Som det fremgår af planchen er amplitudens overgangskurve (roll-off) særdeles jævn. Bessel filtret kendetegnes ved maksimal flad gruppeløbstid (group delay), hvilket betyder at man undgår impulsforvrængning og overhævning (overshoot), ligesom filtret har næsten konstant gruppeforsinkelse for alle passbands. Summa summarum et velegnet filter til hi-fi gengivelse.
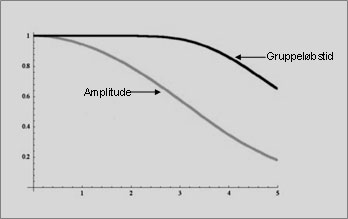
Planche nr. 55 - Bessel 4.ordens filter: Amplitude (gain) og gruppeløbstid (group delay).
Linkwitz-Riley filtre findes kun som 2. ordens og 4. ordens filter, idet de er sammensat af to henholdsvis 1. ordens og 2. ordens Butterworth filtre. Sammensætningen er udført i en kaskadekobling, hvilket vil sige en serieforbindelse af de to Butterworth filtre, hvor det ene filters polaritet er vendt 180 grader i forhold til det andet. Herved ophæves faseforvrængning for det samlede filter. Linkwitz-Riley filtres knækfrekvenspunkt vil grundet sammensætningen af de to Butterworth filter forskydes til – 6 dB.
Faseforvrængning i højere ordens filtre, f.eks. Butterworth, medfører en uheldig påvirkning af disse højttaleres udstrålingskarakteristik.
Faseforvrængning vil medføre løbetidsforvrængning i ”crossover regionen”, hvor f.eks. mellemtone- og diskanthøjttalere overlapper hinanden og udstråler det samme frekvensområde (se 5. del, planche nr. 30 og 31). Dette forårsager mere eller mindre udligning af visse frekvenser, som igen kan føre til ukontrollable ”sidelobes” i retningskarakteristikken for det totale højttalersystem.
På nedenstående plancher ses udstrålingsaksen (rød pil). Med Butterworth filter peger pilen 15 grader nedad i forhold til vandret, forårsaget af faseforvrængning i filtret.
Med anvendelse af Linkwitz-Riley filter bliver udstrålingsaksen rette op til vandret. De to”sidelobes” samt udfasning ved 30 grader (op/ned) ses stadig, men dette skyldes den fysiske afstand mellem diskant og bas-melletonehøjttalerne, - altså ikke faseforvrængning.
Udstrålingskarakteristikker for tovejshøjttalere med en delefrekvens på 2000 Hz:
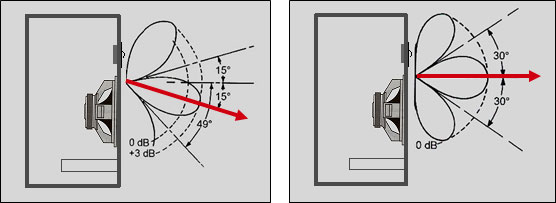
Til venstre: Planche nr. 56 - Butterworth filter. Til højre: Planche nr. 57 - Linkwitz-Riley filter.
Sum summarum Linkwitz-Riley filtre er velegnede til hi-fi gengivelse, hvor specielt 4. ordensfiltret ofte ses anvendt i high-end systemer.
Computerberegninger af korrektionskredsløb:
Det næste vi kan bruge computeren til er beregning af tre typer korrektionskredsløb: Dæmpeled (L-pad) til mellemtone og diskant, Impedans korrektion (Zobel) samt notch filter (LCR sugekreds). En del filterprogrammer indeholder typisk beregninger af de to første kredsløb, hvorimod
beregning af notch filtret ofte er udeladt. Excel regneark til beregning af Notch filtre kan downloades her! Husk brug af notch filtre kræver præcision, hvorfor det kan anbefales at efterkontrollere om computerberegningerne har sammenfald med hensigten. Efterkontrollen kan kun udføres med måleapparatur.
Computeren kan også gøre sig nyttig med andet end måling og beregning i forbindelse med højttalerbyg, f.eks. nedenstående eksempler og flere kan sikkert tilføjes:
Tegneprogrammer til kabinetter: AutoCAD og Solid Works (for de øvede) - eller Google gratis program: http://sketchup.google.com
Uddybende informationer og faglitteratur: Internet, Google, Wikipedia m.m.
Epilog
Som tidligere antydet kan man hurtigt blive opslugt af computerens fantastiske univers. Computeren er en snigende isme, hvor ens begejstring for dens kunnen som værktøj risikerer at få overtaget, - overtaget over sjælen i ”det at bygge højttalere”, hvor menneskelige aspekter som kreativitet, godt håndværk og lytning til musik lader sig overskygge af teknik, tal og formler.
Find balancen!
Copyright © Arne Rodahl 2007
Eftertryk og erhvervsmæssig udnyttelse
uden forfatterens godkendelse er ikke tilladt.
|